PD Dr. Christine Gaßner

Theoretische Informatik  (letztmalig: SoSe 2023)

Berechenbarkeitstheorie über algebraischen Strukturen  (letztmalig: SoSe 2023)

Berechenbarkeitstheorie (letztmalig: SoSe 2023)

Algorithmik und Komplexitätstheorie (letztmalig: WiSe 2022/2023)

Mathematische Logik (letztmalig: WiSe 2021/2022)

Maß- und Integrationstheorie  (letztmalig: WiSe 2015/2016)

Graphentheorie (letztmalig: WiSe 2015/2016)

Praxis des Programmierens (letztmalig: WiSe 2012/2013)

Berechenbarkeitstheorie (letztmalig: WiSe 2022/2023)

Mengenlehre und Prädikatenlogik (letztmalig: WiSe 2022/2023)

NP-vollständige Probleme (letztmalig: SoSe 2022)

Mengenlehre (letztmalig: WiSe 2021/2022)

Das Auswahlaxiom (letztmalig: WiSe 2019/2020)

Berechenbare Analysis (letztmalig: WiSe 2018/2019)

Fundamente der Mathematik (letztmalig: SoSe 2018)

Grenzen der Mathematik (letztmalig: SoSe 2018)

NP-vollständige Probleme der Graphentheorie (letztmalig: WiSe 2017/2018)

DNA Computing (letztmalig: WiSe 2015/2016)

Ausgewählte Themen mit Bezug zur Prädikatenlogik (letztmalig: WiSe 2014/2015)

^{_{Quellen: U. Schöning: Theoretische Informatik - kurz gefasst. N. Blum: Theoretische Informatik: eine anwenderorientierte Einführung.  Duden Informatik. D. Hoffmann: Theoretische Informatik. C.H. Papadimitriou: Computational complexity. K.R. Reischuk: Komplexitätstheorie - Band I: Grundlagen: Maschinenmodelle, Zeit- und Platzkomplexität, Nichtdeterminismus.}}

Grundbegriffe
Kodierungen
Der Begriff Algorithmus
Gödelisierungen
Grammatik und Sprachen
Erzeugung von Sprachen (Beispiele)
Erweiterte Transformationsrelation
Weitere Beispiele und Syntaxbäume
Die Chomsky-Hierarchie
Erkennbarkeit und Entscheidbarkeit (Vorbereitung)
Erkennbarkeit und Entscheidbarkeit (Der Satz 2.1)
Erkennbarkeit und Entscheidbarkeit (Die Satz 2.2 und Satz 2.3)
Erkennbarkeit und Entscheidbarkeit (Zum Beweis von Satz 2.3, Veranschaulichung)
Korrektur 3:17 ... jede Kette, die durch Pfeile veranschaulicht ...
Erkennbarkeit und Entscheidbarkeit (Der formale Beweis von Satz 2.3)
Endliche Automaten (Definition und Beispiele)
Endliche Automaten und Typ-3-Sprachen
Reguläre Ausdrücke (Teil 1)
Reguläre Ausdrücke (Teil 2)
Pumping Lemmata (Typ 2 und Typ 3)
Hinweis: Präzisierung (etwa ab 18:05 min):
1)   Ein Binärbaum der Tiefe k hat höchstens 2^k Blätter.
2)   Ein  vollständiger Binärbaum der Tiefe k (d.h. ein Baum,
      in dem alle Wege von der Wurzel zu den Blättern die Tiefe k haben)
      hat genau 2k Blätter.
Nichtdeterministische Kellerautomaten (Teil 1)
Nichtdeterministische Kellerautomaten (Teil 2)
Hinweis: Die Folien 165 und 166 wurden nachträglich korrigiert: H3 wurde neu eingefügt.
Turingmaschine
Das Halteproblem
Deterministische Kellerautomaten und die Chomsky-Hierarchie
Die Mehrband-Turingmaschine
LOOP-Programme
WHILE-Programme
Die Ackermannfunktion
GOTO-Programme
Partiell rekursive Funktionen
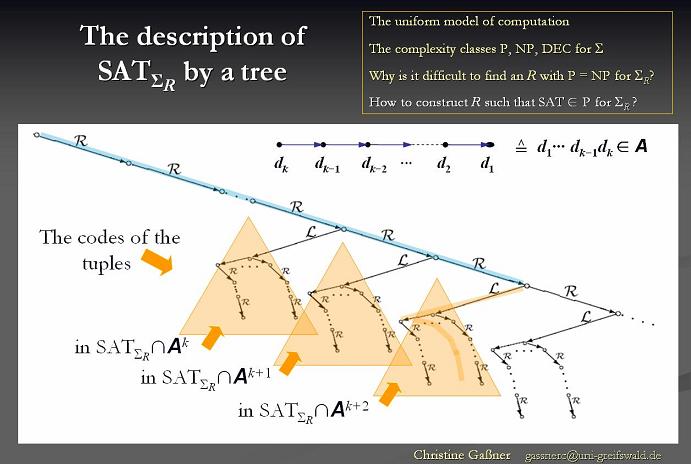
Komplexität und das Erfüllbarkeitsproblem